We consider cubature rules of precision or degree d of the form
 |
Bn | w(x) f(x) dV = IN[f] + RN[f] (1) |
where Bn is a region in n-dimensional Euclidean
space En,
x := ( x1, ..., xn )
is a point in En,
dV is an element of volume in
En, w
is a weight function,
| IN f := | 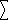 | N
i = 1 | wi f(xi), wi  0, i = 1, ..., N (2) 0, i = 1, ..., N (2) | |
is a cubature rule and
RN f is the remainder which has the property that
RN f = 0 if f
is a linear combination of monomials of the form
 | n
j = 1 | xji | with |
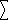 | n
j = 1 | ij  d d | and |
RN f  0 for some such monomial with 0 for some such monomial with
| 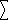 | n
j = 1 | ij = d + 1. | |
The regions Bn
which we include in our compilation are the three
bounded regions Cn, the hypercube,
Sn, the hypersphere and
Tn, the simplex and
the entire space En.
Associated with the
bounded regions is the weight function w(x)  1
while with En, we associate two weight functions, exp(-r)
and exp(-r2) where
1
while with En, we associate two weight functions, exp(-r)
and exp(-r2) where | r2 := | 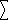 | n
j = 1 | xj2 . |
As in [Str71],
En with these two weight functions is denoted by Enr and
Enr2, respectively.
The definitions of the bounded regions are given by
Cn : -1  xj xj  1, j = 1, ..., n 1, j = 1, ..., n
|
Sn :
r2  1
1 |
| Tn : | 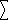 | n
j =
1 | xj  1, xj 1, xj  0, j = 1, ..., n
. 0, j = 1, ..., n
. | |
A more detailed description of the regions we consider is given
here.
As a general rule
we do not include cubature rules of degree 2m - 1 which
use more than mn points since the (Cartesian, Spherical or Conical)
product Gaussian rule of
degree 2m - 1 requires mn points and is usually superior to any
other cubature rule of the same degree. This also holds true for the top of an
embedded sequence since there is a very good way to generate an embedded
sequence starting with a product Gaussian rule and generating cubature
rules of
lower degree in an optimal manner [CH89].
Exceptions to this rule are cubature rules with properties that some users may desire,
such as equal weights, points on the boundary or more symmetry.
This page was last modified on Monday 17 June 2002, 15:13:42 CEST.
